Binary Search

Binary Search Explained

Binary Search is a searching algorithm used in a sorted array by repeatedly dividing the search interval in half.

The idea of binary search is to use the information that the array is sorted and reduce the time complexity to $\mathcal{O}(\log n)$.

The basic steps to perform Binary Search are:

1. Begin with an interval covering the whole array.
2. If the value of the search key is less than the item in the middle of the interval, narrow the interval to the lower half.
3. Otherwise, narrow it to the upper half.
4. Go back to Step 2 until the value is found or the interval is empty.

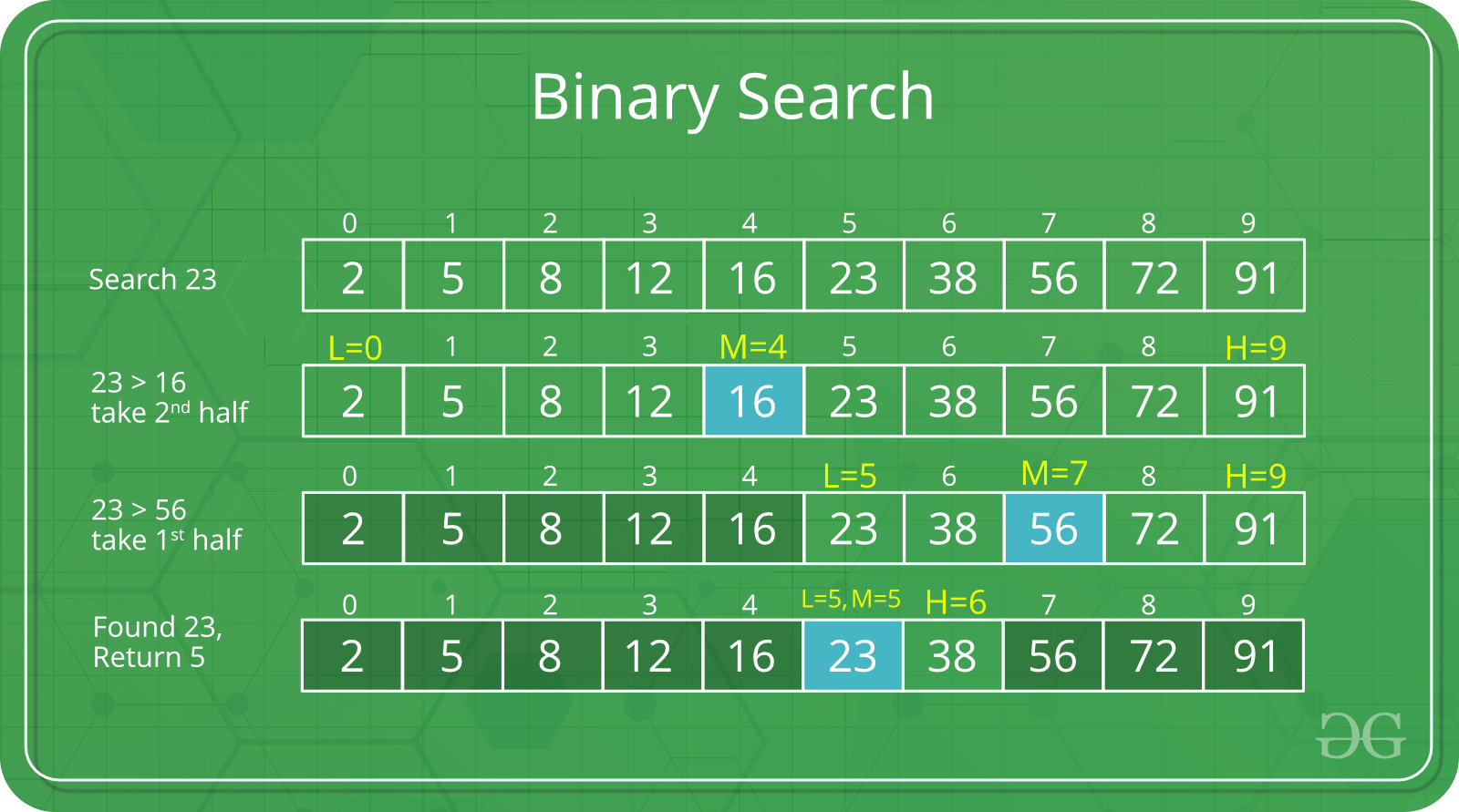Image from GeeksforGeeks

Implementation

There's... actually a built-in function defined in header <algorithm> (std::binary_search). There's really no need to write your own. You can read more about it here.

Ok. I get it. You just feel restless and geeky and want to write your own Binary Search function.

Code

Here you go nerds:

Iteration method

// Binary Search in C++

#include <iostream>
using namespace std;

int binarySearch(int array[], int x, int low, int high) {

  // Repeat until the pointers low and high meet each other
  while (low <= high) {
    int mid = low + (high - low) / 2;

    if (array[mid] == x)
      return mid;

    if (array[mid] < x)
      low = mid + 1;

    else
      high = mid - 1;
  }

  return -1;
}

Recursion is basically running a code again and again until you get the desired results. For example:

#include <bits/stdc++.h>
using namespace std;
int meg(int n, int peaches) {
  if (n == 0)
    return peaches;
  peaches = (peaches + 1) * 2;
  return meg(n - 1, peaches);
}
int main() {
  int peaches = 1;
  int n;
  cin >> n;
  cout << meg(n, peaches);
}

This is a recursive binary search algorithm

int binarySearch(int array[], int x, int low, int high) {
  if (high >= low) {
    int mid = low + (high - low) / 2;

    // If found at mid, then return it
    if (array[mid] == x)
      return mid;

    // Search the left half
    if (array[mid] > x)
      return binarySearch(array, x, low, mid - 1);

    // Search the right half
    return binarySearch(array, x, mid + 1, high);
  }

  return -1;
}